MATEMÁTICA LEGAL
Um site que nos mostrará um pouco sobre a matemática e sua realidade na vida dos alunos.
terça-feira, 25 de abril de 2023
domingo, 11 de março de 2018
GEOMETRIA ANALÍTICA
AVALIAÇÃO CONTÍNUA ESTÁ CHEGANDO!!!
SIMULADO ESTÁ CHEGANDO!!!
QUERO DESAFIAR AS TURMAS DOS OITAVOS ANOS A ESTUDAREM O MATERIAL ABAIXO E SE DESTACAREM NO 1° SIMULADO DO ANO.
PONTOS , RETAS E PLANOS
AULÃO SOBRE PONTOS, RETAS E PLANOS
ANEXO - PONTOS,RETAS E PLANOS
SIMULADO ESTÁ CHEGANDO!!!
QUERO DESAFIAR AS TURMAS DOS OITAVOS ANOS A ESTUDAREM O MATERIAL ABAIXO E SE DESTACAREM NO 1° SIMULADO DO ANO.
PONTOS , RETAS E PLANOS
AULÃO SOBRE PONTOS, RETAS E PLANOS
ANEXO - PONTOS,RETAS E PLANOS
POTENCIAÇÃO - 8° ANO
APROVEITEM E PRATIQUEM BASTANTE!!!!!
AULA EM PDF SOBRE POTENCIAÇÃO
Potenciação pdf
EXERCÍCIO EXTRA
Exercício Extra
ATIVIDADE COMPLEMENTAR - 7° ANO
MÁXIMO DIVISOR COMUM
O máximo divisor comum, ou MDC, de dois ou mais números inteiros é o maior divisor inteiro comum a todos eles. Por exemplo, o m.d.c. de 16 e 36 é o 4, e denotamos isso por MDC 16, 36 = 8. Já o MDC de 30, 54 e 72 é o 6, o que é denotado por MDC 30, 54, 72 = 6.
Propriedades do MDC:
- Quando fatoramos dois ou mais números, o MDC deles é o produto dos fatores comuns a eles, por exemplo o MDC de 12 e 18 é 6
- Quando temos dois números consecutivos entre si, podemos concluir que o MDC deles é 1, uma vez que eles serão sempre números primos. Por exemplo: 25 e 26 (o maior número que divide ambos é o 1)
- Quando temos dois ou mais números e um deles é divisor dos outros, podemos concluir que ele é o MDC dos números, por exemplo, 3 e 6. (se 3 é divisor de 6, ele é o MDC de ambos)
Como calcular o MDC?
Para calcular o máximo divisor comum (MDC) entre números, devemos realizar a fatoração por meio da decomposição dos números indicados.
Para exemplificar, vamos calcular através da fatoração o MDC do 20 e 24:
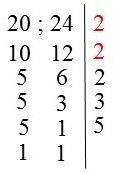
Para saber o MDC dos números, devemos olhar a direita da fatoração e ver quais números dividiram simultaneamente os dois e multiplicá-los.
Assim, pela fatoração podemos concluir que o 4 (2x2) é o maior número que divide ambos e, portanto, é o máximo divisor comum de 20 e 24.
Exemplos
1. Qual o MDC de 18 e 60?
Pela fatoração de ambos os números temos:

Ao multiplicar os números que dividem ambos, temos que o MDC de 18 e 60 é 6 (2 x 3).
2. Qual o MDC de 6; 12 e 15?
Pela fatoração dos números temos:
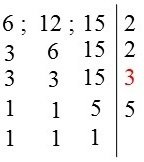
Logo, temos que o MDC de 6; 12 e 15 é 3.
ATIVIDADE EXTRA - NÚMEROS DECIMAIS
NÚMEROS DECIMAIS;
Números decimais são números que possuem vírgula, por exemplo, 2,35; 1,2; 0,25. Ao lermos esses números falamos o seguinte, por exemplo:
1,5 = temos o costume de ler “um vírgula cinco”, mas matematicamente está incorreto. Para fazer a leitura corretamente de um número decimal devemos saber algumas definições.
Todo número que é escrito na forma decimal pode ser transformado em fração, isso é através da decomposição do número decimal transformamos-os em fração, veja como:
5,2----- 5 é a parte inteira do número e 2 é a parte decimal, então se somarmos a parte inteira com a decimal resultamos no número 5,2.
5 + 0,2 = 5,2. O número 0,2 continua decimal, então para transformá-lo em fração vamos reparar que ele não possui parte inteira, apenas parte decimal a qual é composta por apenas um número, então 0,2 é o mesmo que
2 .
10
Podemos então dizer que 5,2 = 5 + 0,2 , com base nessa soma dizemos que a leitura de 5,2 ficará assim: cinco inteiros e dois décimos.
Veja alguns exemplos abaixo:
2,1 = dois inteiros e um décimo.
0,36 = trinta e seis centésimos.
2,36 = dois inteiros e trinta e seis centésimos.
14,6 = quatorze inteiros e seis décimos.
ACHEI INTERESSANTE POSTAR ESSAS INFORMAÇÕES ABAIXO:
APROVEITE E BOM ESTUDO !!!!!!
NO SITE
https://brasilescola.uol.com.br/matematica/operacoes-com-numeros-decimais.htm

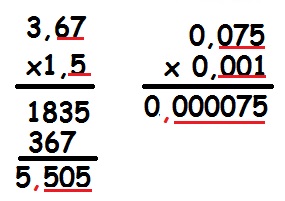
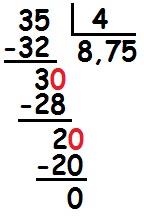


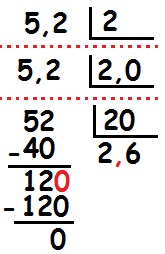
ATIVIDADE EXTRA - NÚMEROS DECIMAIS 1
ATIVIDADE EXTRA - NÚMEROS DECIMAIS 2
OS LINKS PARA AS ATIVIDADES ESTÃO ACIMA.
Números decimais são números que possuem vírgula, por exemplo, 2,35; 1,2; 0,25. Ao lermos esses números falamos o seguinte, por exemplo:
1,5 = temos o costume de ler “um vírgula cinco”, mas matematicamente está incorreto. Para fazer a leitura corretamente de um número decimal devemos saber algumas definições.
Todo número que é escrito na forma decimal pode ser transformado em fração, isso é através da decomposição do número decimal transformamos-os em fração, veja como:
5,2----- 5 é a parte inteira do número e 2 é a parte decimal, então se somarmos a parte inteira com a decimal resultamos no número 5,2.
5 + 0,2 = 5,2. O número 0,2 continua decimal, então para transformá-lo em fração vamos reparar que ele não possui parte inteira, apenas parte decimal a qual é composta por apenas um número, então 0,2 é o mesmo que
2 .
10
Podemos então dizer que 5,2 = 5 + 0,2 , com base nessa soma dizemos que a leitura de 5,2 ficará assim: cinco inteiros e dois décimos.
Veja alguns exemplos abaixo:
2,1 = dois inteiros e um décimo.
0,36 = trinta e seis centésimos.
2,36 = dois inteiros e trinta e seis centésimos.
14,6 = quatorze inteiros e seis décimos.
ACHEI INTERESSANTE POSTAR ESSAS INFORMAÇÕES ABAIXO:
APROVEITE E BOM ESTUDO !!!!!!
NO SITE
https://brasilescola.uol.com.br/matematica/operacoes-com-numeros-decimais.htm
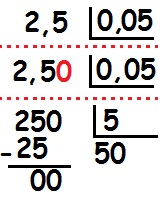
Quando desejamos realizar operações de adição ou de subtração, podemos utilizar o algoritmo de cada operação. Mas devemos nos lembrar de que a parte inteira deve somar apenas com outra parte inteira, do mesmo modo a parcela decimal deve ser operada com a outra que também é decimal. Para evitar enganos, é recomendável que façamos o algoritmo colocando sempre a vírgula embaixo de outra vírgula. Vejamos alguns exemplos:

Na imagem, temos alguns “zeros” em vermelho. Isso aconteceu porque nem sempre todos os números terão a mesma casa de números decimais e, a fim de melhorar nossos cálculos, devemos preencher com zeros os espaços vazios à direita.
Em se tratando de multiplicação, não há a necessidade de colocarmos vírgula embaixo de vírgula. Devemos realizar a multiplicação da forma tradicional, mas devemos lembrar que é necessário unir a quantidade de casas decimais. Por exemplo, o caso da multiplicação de 0,075 por 0,001. Ao fazermos a multiplicação normalmente, desconsiderando a vírgula, obtemos o resultado 75, mas o primeiro número tem três algarismos após a vírgula, e o segundo, três algarismos. Portanto, a resposta é 0,000075. Vejamos alguns exemplos:
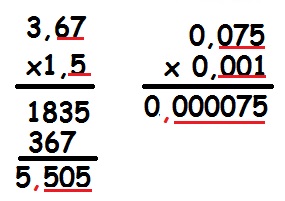
A divisão de números inteiros requer a nossa atenção para alguns detalhes. Vejamos os possíveis casos de divisões:
1º – Divisão de números inteiros
a) Quando o dividendo é maior que o divisor:
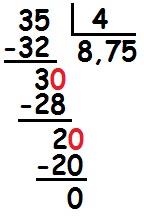
Nesse caso, poderíamos ter finalizado a divisão tendo como quociente o número 8 e deixando 3 como resto. Como demos continuidade, foi necessário acrescentar o zero ao fim dos números que seriam divididos para concluir a divisão. Quando é necessário fazer o acréscimo do zero, colocamos uma vírgula no quociente.
b) Quando o dividendo é menor que o divisor:

Nesse exemplo, queremos dividir 4 por 8. Mas para conseguir fazer esse cálculo, é necessário aumentar o dividendo. Então antes de iniciar a divisão, precisamos acrescentar um zero após o 4, transformando-o em 40. Ao fazer isso, colocamos um zero e uma vírgula no início do quociente para em seguida iniciar de fato a divisão. Caso fosse necessário, poderíamos colocar outro zero no dividendo, então haveria 400, e, no quociente, acrescentar outro zero após a vírgula, ficando com 0,0. É possível realizar esse processo quantas vezes forem necessárias.
2º – Divisão entre inteiros e decimais
a) Dividendo inteiro e divisor decimal

Quando precisamos dividir um número inteiro por outro que é decimal, é necessário tornar o dividendo também um número decimal. Para isso, basta acrescentar uma vírgula e um zero e verificar se o dividendo e o divisor possuem a mesma quantidade de números após a vírgula. Se for necessário, podemos acrescentar zeros até ficarem iguais. Feito isso, desconsideramos a vírgula e realizamos a divisão normalmente.
a) Dividendo decimal e divisor inteiro
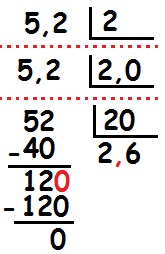
Semelhantemente ao caso anterior, precisamos que o divisor seja também um número decimal. Para tanto, acrescentamos nele a vírgula e um zero e verificamos se a quantidade de zeros após a vírgula é mesma para o divisor e para o dividendo. Feito isso, podemos realizar a divisão como de costume.
3º – Divisão entre decimais
Para realizar a divisão entre números decimais, é necessário que ambos tenham a mesma quantidade de números após a vírgula. Como já foi dito, acrescentamos zeros ao fim do número até que consigamos igualar a quantidade de casas decimais. Feito isso, desconsideramos as vírgulas e realizamos a divisão.

ATIVIDADE EXTRA - NÚMEROS DECIMAIS 1
ATIVIDADE EXTRA - NÚMEROS DECIMAIS 2
OS LINKS PARA AS ATIVIDADES ESTÃO ACIMA.
IMPORTANTE!!!!
LEMBRETE!!!!!!!
Assinar:
Postagens (Atom)









